在量子力学的神秘世界中,二能级系统是一个基础而重要的研究对象。它不仅在理论上提供了一个简化的模型来理解量子现象,而且在实际应用中,如量子计算和量子通信等领域扮演着关键角色。《张朝阳的物理课》深入浅出地介绍了二能级系统的基本概念及其能量本征态的求解方法,本文将围绕这一主题进行详细阐述。
二能级系统,顾名思义,是指量子系统中只包含两个能级的系统。这两个能级可以是原子中的电子能级,也可以是量子比特中的两个状态。在量子力学中,系统的能量状态由波函数描述,而波函数满足薛定谔方程。对于二能级系统,其哈密顿量通常可以写成一个2×2的矩阵形式。
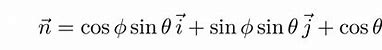
在二能级系统中,哈密顿量H通常包含两部分:一个描述系统静态能级的对角项,和一个描述能级间相互作用的非对角项。对于一个简化的模型,哈密顿量可以表示为:
\[ H = \begin{pmatrix} E_1 & V \\ V^* & E_2 \end{pmatrix} \]
其中,\( E_1 \)和\( E_2 \)是两个能级的能量,\( V \)是能级间的耦合强度。
为了求解二能级系统的能量本征态,我们需要解薛定谔方程:
\[ H\psi = E\psi \]
其中,\( \psi \)是系统的波函数,\( E \)是能量本征值。将哈密顿量代入上述方程,我们得到一个关于波函数的线性方程组。通过求解这个方程组,我们可以得到能量本征值和对应的波函数。
能量本征值可以通过求解哈密顿量的特征值问题得到。将哈密顿量写成特征值问题的形式:
\[ \det(H EI) = 0 \]
其中,\( I \)是单位矩阵。解这个方程,我们可以得到两个能量本征值:
\[ E_{\pm} = \frac{E_1 E_2}{2} \pm \sqrt{\left(\frac{E_1 E_2}{2}\right)^2 |V|^2} \]
这两个能量本征值对应着系统的两个可能的能量状态。
得到能量本征值后,我们可以进一步求解对应的波函数。将能量本征值代入薛定谔方程,解出波函数:
\[ \psi_{\pm} = \begin{pmatrix} \cos(\theta/2) \\ \pm e^{i\phi}\sin(\theta/2) \end{pmatrix} \]
其中,\( \theta \)和\( \phi \)是两个角度参数,可以通过能量本征值和耦合强度计算得出。
通过《张朝阳的物理课》的介绍,我们不仅学习了二能级系统的基本概念,还掌握了如何求解其能量本征态的方法。这一过程不仅加深了我们对量子力学基本原理的理解,也为进一步探索量子世界的奥秘奠定了基础。二能级系统的研究不仅具有理论价值,更在实际应用中展现出巨大的潜力,如在量子计算和量子通信技术中的应用,预示着未来科技的无限可能。
诗画悠远流长。
2025-03-31 10:43:09
2025-03-31 09:56:02
2025-03-31 09:08:45
2025-03-31 08:21:33
2025-03-31 07:34:29
2025-03-31 06:47:20
2025-03-31 06:00:07
2025-03-30 18:33:26
发表评论